第二章：信息的表示和处理

不同于原书籍，笔记从信息存储、整型编码与运算、浮点编码与运算共三节进行概括。以便加强自身记忆以及自己日后查阅。总的来说，本章要研究如何在有限的空间里表示数。

2.1 信息存储

2.1.1 数据大小

Typical sizes (in bytes) of basic C data types
C declaration		Bytes
Signed	Unsigned	32-bit	64-bit
char	unsigned char	1	1
short	unsigned short	2	2
int	unsigned int	4	4
long	unsigned long	4	8
int32_t	uint32_t	4	4
int64_t	uint64_t	8	8
char*	/	4	8
float	/	4	4
double	/	8	8

值得一提的是，char*指针在32位系统是以4字节存的，而在64位系统中是以8字节存的。这是因为32位系统的虚拟内存地址是32位的，而64位系统是64位的。也就是说，32位系统的最大寻址空间是2的32次方，约4GB；而64位系统寻址范围理论可上亿GB。该内容应该与体系结构有关，暂时做了解即可。（P.S. 1字节byte是8位，也就是8比特bit）

2.1.2 大小端

大端模式(Big endian)，是指数据的高字节保存在内存的低地址中，而数据的低字节保存在内存的高地址中。这和我们的阅读习惯一致。小端模式(Little endian)，是指数据的高字节保存在内存的高地址中，而数据的低字节保存在内存的低地址中。

比如说int0x1234567储存在地址0x100，这意味着：

地址	0x100	0x101	0x102	0x103
大端	01	23	45	67
小端	67	45	23	01

顺带一提，Intel的X86架构是小端模式。

2.1.3 运算

2.1.3.1 位级运算

位级运算就是利用布尔运算来处理比特串。常见有掩码运算，如x&0xFF保持最低位字节不变，其他字节清零。

一些符号
逻辑运算	布尔运算	命题逻辑
NOT(非)	~	￢
AND(与)	&	^
OR(或)	\|	∨
XOR(异或)	∧	⊕

离散应该会讲的吧。

2.1.3.2 逻辑运算

就是||、&&以及!
返回0x01与0x00，不多赘述。

2.1.3.3 移位运算

若x的位表示为[x_w-1,x_w-2,...,x₀]，则：

左移x << k为[x_w-k-1,x_w-k-2,...,x₀,0,0,...,0]
逻辑右移x >> k为[0,0,...,0,x_w-1,x_w-2,...,x_k]
算术右移x >> k为[x_w-1,x_w-1,...,x_w-1,x_w-2,...,x_k]

对于符号整数采用算术右移，无符号整数采用逻辑右移。(这与二进制补码有关，至少算术右移可以保证符号整数的正负不变)

2.2 整型编码与运算

2.2.1 整型编码

若以w长度空间储存的整型x的位表示为[x_w-1,x_w-2,...,x₀]，则：

若x为无符号整数，则x = Σ(i=0~w-1)2ⁱx_i
若x为符号整数（二进制补码），则x = -x_w-12^w-1 + Σ(i=0~w-2)2ⁱx_i

2.2.2 整型之间的转换

核心在于位表示不变！（还是比较直观的，不高兴举例子了。总之若存储空间大小不变，那bit pattern就不变，管他有无符号；若存储空间变小，那就把草率地把前面多余的比特扔掉；如果存储空间变大，如果是有符号的，就用x_w-1来填充前面多出来的空间，如果无符号，就用0来填充。（这里的“前面”指的是数据的高字节，也就是左边的数码

2.2.3 整型运算

2.2.3.1 加法运算

核心仍然在于位表示不变！加法所导致溢出的位就扔掉就好了。如[1010] + [0111] = [0001] = 1

2.2.3.2 取负数

出发点要满足：x + (-x) = 0。因此对于w长度存储空间的整数x：

若x为无符号整数，则-x = 2^w - x（x > 0时），或-x = 0（x = 0时）
若x为符号整数，则-x = -x （x > min），或-x = min（x = min）。其中min为w位二进制补码所能表示的最小值

2.2.3.3 乘法运算

依旧还是位表示不变。无论有无符号，只需算出正确答案，再把超出储存空间的位扔掉，就OK了。真正让我们感兴趣的是通过移位运算来解决乘以常数的问题。

比如说：x * 6 = (x << 2) + (x << 1)；x * 31 = (x << 5) - x

移位运算能被简单的实现。一般来说，编译器会自己帮我们做这种优化。

2.2.3.4 除法运算

整型除法运算都要向零方向去近似（round toward zero）。也就是说-5/2 = -2、5/2 = 2。负数向上取整，正数向下取整。对于除以2的幂，我们依旧可以用移位来优化，而任意的常数却无能为力。

对于结果为负数的除法，为了满足向上取整，需要引入一个偏置(1 << k) - 1。比如说(short)-12340/256 = -48，然而-12340 >> 8 = [1100111111001100] >> 8 = [1111111111001111] = -49不满足结果。但是引入偏置后(x + (1 << k) - 1) >> k = [1101000011001011] >> 8 = [1111111111010000] = -48满足结果。

2.3 浮点编码与运算

2.3.1 IEEE浮点表示

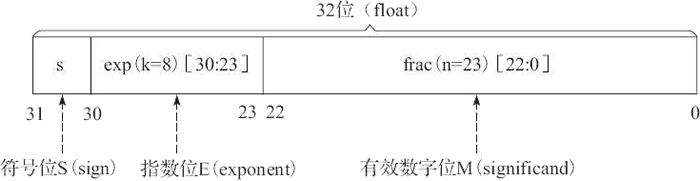
IEEE浮点数标准是从逻辑上用三元组{S，E，M}来表示一个数V的，即V = (-1)^s×M×2^E。其中s(sign)是符号位， M(significand)是尾数位，E(exponent)是阶码。IEEE浮点数标准规定了单精度和双精度浮点格式。C语言中分别叫float和double。s = 1为负，s = 0为正。 exp当作无符号整型再减去偏置Bias得到E，Bias = 2^k-1-1，k是exp的位数。偏置Bias的引入为了解决负指数问题。frac为二进制小数的小数部位。比如[10100,...,0] = 0.5 + 0.125 = 0.625。frac还需进行一些简单运算可得M。

根据exp的值，编码可以分为三种类型——规格化值、非规格化值和特殊值。下以单精度浮点数为例。

规格化值：exp既不全为0也不全为1。E = exp - Bias，M = frac + 1。
非规格化值：exp全为0。E = 1 - Bias，M = frac。可以表示0以及接近0的数。
特殊值：exp全为1。若frac全为零，V表示无穷大；若frac不全为零，V是NaN(not a number)。

顺带一提，之所以让非规格化的E为1-Bias而不是-Bias是为了数较小的非规格化数集到数较大的规格化数集的平稳过渡。

2.3.2 浮点数的舍入

默认采用向偶舍入的方法。就是四舍六入五凑偶，与物理实验数据处理一致。不赘述了。

2.3.3 浮点数的运算

浮点数的运算不满足结合律和分配律。（认为例子中的1e20为float）如：(3.14 + 1e20) - 1e-20 = 0.0，而3.14 + (1e20 - 1e20) = 3.14；1e20 * (1e20 - 1e20) = 0，而1e20 * 1e20 - 1e20 * 1e20 = NaN。总之，浮点运算难免会产生精度上的误差。