第五章：优化程序性能

5.1 编译器的能力和局限性

第三章讨论过compiler可以自己优化代码，但是这种优化必定是安全的。因此有两种optimization blocker是不会被compiler所优化——memory aliasing、function call。

5.1.1 memory aliasing

void twiddle1(long *xp, long *yp)
{
    *xp += *yp;
    *xp += *yp;
}
void twiddle2(long *xp, long *yp)
{
    *xp += 2 * *yp;
}

twiddle1需要6次内存引用（2次读取yp、2次读取xp和2次写xp），twiddle2只需要3次（1次读取yp，1次读取xp和1次写xp）。但是当xp与yp一致时，twiddle1与twiddle2结果不同。 因此编译器不会将twiddle1优化成twiddle2。即便程序里不存在memory aliasing，编译器也不敢贸然优化。

5.1.2 function call

long f();
long func1()
{
    return f()+f()+f()+f();
}
long func2()
{
    return 4*f();
}

func1需要四次函数调用，func2只需要一次。但是编译器不会将func1优化成func2，考虑如下的f()：

long count = 0;
long f()
{
    return count++;
}

显然func1与func2结果不同。即便程序里不存在这么特殊的f()，编译器也不敢贸然优化。

5.2 CPE: Expressing Program Performance

不同于学习算法时，利用大O表示法来描述performance，我们利用cycles per element, abbreviated CPE，来描述performance。 书上似乎没有讲如何测量CPE，我们也不深究测量方法了。

第四章有讲过CPU的时钟周期cycle，这里再顺带一提默频、睿频的含义。比如我现在所用的i7-9850H的默频是2.6GHz，也就是默认的CPU的时钟一秒钟经历2.6GHz。 现在的速度是0.88GHz，也就是实际CPU主频只有0.88GHz，毕竟只是在打字。睿频是一种技术，使得CPU的时钟频率可以超越默频。

5.3 一个例子引发的血案

现有一个vector类，现在想要把vector里面的所有元素进行OP运算，并把结果存在*dest，OP可能是加法也可能是乘法。 当OP是加法时，IDENT等于0；当OP是乘法时，IDENT等于1。vec_ptr是指向vector类的指针。data_t可能是long也可能是double。

朴素的combine1

void combine1(vec_ptr v, data_t *dest)
{
    long i;

    *dest = IDENT;
    for (i = 0; i < vec_length(v); i++) {
        data_t val;
        get_vec_element(v, i, &val); //将v中的第i个元素存在&val里
        *dest = *dest OP val;
    }
}

减少function call的combine2

显然combine1每次for循环均要调用vec_length，而vector长度并不改变，陷入了5.1.2function call的optimization blocker之中。修改如下：

void combine2(vec_ptr v, data_t *dest)
{
    long i;
    long length = vec_length(v);
    
    *dest = IDENT;
    for (i = 0; i < length; i++) {
        data_t val;
        get_vec_element(v, i, &val);
        *dest = *dest OP val;
    }
}

再次减少function call但似乎无用的combine3

combine2的for循环中get_vec_element()被多次调用，考虑通过vector分装的数组来绕过该函数调用。虽然这种方法违背了分装。。。

void combine3(vec_ptr v, data_t *dest)
{
    long i;
    long length = vec_length(v);
    data_t *data = get_vec_start(v); //获得v的第一个元素地址，接下来便可寻秩遍历了。
    
    *dest = IDENT;
    for (i = 0; i < length; i++) {
        *dest = *dest OP data[i];
    }
}

奇怪的事情发生了，combine3性能比combine2要差，这说明循环中的其他操作才是瓶颈。

减少内存引用的combine4

之前所有的代码for循环中都是反复读取并写入dest指针指向的内存，造成了时间的浪费。修改如下：

void combine4(vec_ptr v, data_t *dest)
{
    long i;
    long length = vec_length(v);
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;
    
    *dest = IDENT;
    for (i = 0; i < length; i++) {
        acc = acc OP data[i];
    }
    *dest = acc;
}

注意到这里存在着memory aliasing的optimization blocker：当dest指向vector内部的元素时，计算的结果是不同的。编译器自然不会进行类似combine4的优化。

5.4 理解现代处理器

之前combine2、3、4的修改只是针对两个optimization blocker的。想要理解CPE以及进一步优化代码，需要了解处理器的体系结构和其表现出的指令级并行(instruction-level parallelism, 同时对多条指令进行求值)。

5.4节内容许多来自CSAPP：14[VB]优化程序性能。

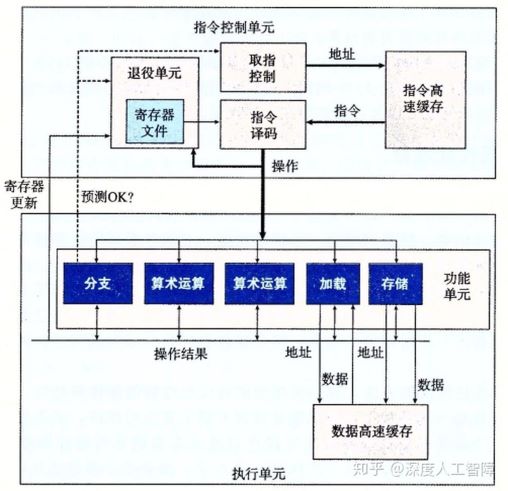
如上图所示是一个简化的Intel处理器的结构，采用了超标量(superscalar)体系结构，意味着处理器可以在每个时钟周期执行多个操作，并且可以乱序(Out-of-order)执行。

5.4.1 该处理器主要由两部分构成：

1）指令控制单元（Instruction Control Unit，ICU）

指令控制单元通过取指控制逻辑（fetch control）从指令高速缓存中读出指令序列，并根据这些指令序列生成一组针对程序数据的基本操作，然后发送到执行单元中。

• 取指控制逻辑：包含分支预测，来完成确定要取哪些指令。 分支预测（Branch Prediction）技术：当程序遇到分支时，程序有两个可能的前进方向，处理器会猜测是否选择分支，同时预测分支的目标地址，直接取目标地址处的指令。
• 指令高速缓存（Instruction Cache）：特殊的高速存储器，包含最近访问的指令。ICU通常会很早就取指，给指令译码留出时间。
• 指令译码逻辑：接收实际的程序指令，将其转换成一组基本操作（微操作），并且可以在不同的硬件单元中并行地执行不同的基本操作。比如x86-64中的addq %rax, 8(%rdx)，可以分解成访问内存数据8(%rdx)、将其加到%rax上、将结果保存会内存中。
• 退役单元（Retirement Unit）：指令译码时会将指令信息放到队列中，确保它遵守机器级程序的顺序语义。队列中的指令主要包含两个状态：
  (a)退役（Retired）：当指令完成，且引起这条指令的分支点预测正确，则这条指令会从队列中出队，然后完成对寄存器文件的更新。
  (b)清空（Flushed）：如果引起该指令的分支点预测错误，就会将该指令出队，并丢弃计算结果，由此保证预测错误不会改变程序状态。
  

2）执行单元（Execution Unit，EU）

执行单元使用投机执行技术执行由ICU产生的基本操作，通常每个时钟周期会接收多个基本操作，将这些操作分配到一组功能单元中来执行实际的操作。

• 投机执行（Speculative Execution）技术：直接执行ICU的预测指令，但是最终结果不会存放在程序寄存器或数据内存中，直到处理器能确定应该执行这些指令。分支操作会被送到EU中来确定分支预测是否正确。如果预测错误，EU会丢弃分支点之后计算出来的结果，并告诉分支模块。
• 功能单元（functional units）：专门用来处理不同类型操作的模块，并且可以使用寄存器重命名机制将“操作结果”直接在不同单元间进行交换，这是数据转发技术的高级版本。
  • 存储模块和加载模块负责通过数据高速缓存来读写数据内存，各自包含一个加法器来完成地址的计算，并且单元内部都包含缓冲区来保存未完成的内存操作请求集合。每个时钟周期可完成开始一个操作。
  • 分支模块：当得知分支预测错误，就会在正确的分支目的中取指。
  • 算数运算模块：能够执行各种不同的操作。
  • 寄存器重命名机制（Register Renaming）：会维护一个寄存器的重命名表来进行数据转发，主要有以下步骤：
    当执行一条更新寄存器r的指令I1，会产生一个指向该操作结果的唯一标识符t，然后将(r, t)加入重命名表中。 当后续有需要用到寄存器r作为操作数的指令时，会将t作为操作数源的值输入到单元中进行执行。 当I1执行完成时，就会产生一个结果(v, t)，表示标识符t的操作产生了结果v，然后所有等待t作为源的操作都会使用v作为源值。
• 数据高速缓存（Data Cache）：存放最近访问的数据值。

5.4.2 功能单元的性能

csapp的参考机Intel Core i7 Haswell算数运算性能如下图所示

• 延迟（Latency）：表示完成单独一个运算所需的时钟周期总数
• 发射时间（Issue Time）：表示采用流水线时，两个连续的同类型运算之间需要的最小时钟周期数
• 容量（Capacity）：表示能够执行该运算的功能单元数量

应该指出，发射时间为1的运算，意味着对应的功能单元是完全流水线化的（Fully Popelined）。除法运算的延迟等于发射时间，意味着需要完全执行完当前的除法运算，才能执行下一条除法运算。 完全流水线化的也就是第四章讨论的情况。

根据以上运算性能，我们可以得到CPE值的两个基本界限，来描述程序的最大性能：

1）延迟界限(latency bound)：

• 意义：当指令存在数据相关时，指令的执行必须严格顺序执行，就会限制了处理器指令级并行的能力，延迟界限就会限制程序性能。
• 解释：当存在数据相关时，指令是严格顺序执行的，意味着我们无法通过指令并行来进行加速。而通过参考机的运算性能知道执行每种运算所需的延迟，就确定了执行该运算所需的最小时钟周期数，此时CPE的延迟界限就是运算操作的延迟。比如整数乘法的延迟为3个时钟周期，意味着我们需要用3个时钟周期才能完成一个整数乘法运算，不可能更快了，所以当前的CPE值为3。

2）吞吐量界限(throughput bound)：

• 意义：刻画了处理器功能单元的原始计算能力，是程序性能的终极限制。
• 解释：表示我们考虑系统中的所有的功能单元，计算出来运算结果的最大速率。比如参考机含有4个可以执行整数加法的功能单元，且整数加法的发射时间为1，所以系统执行整数加法的吞吐量为4，意味着CPE值为0.25，但是参考机中只有两个支持加载的功能单元，意味着每个时钟周期只能读取两个操作数，所以这里的吞吐量就受到了加载的限制，CPE值为0.5。再比如参考机内只含有一个能执行整数乘法的功能单元，说明一个时钟周期只能执行一个整数乘法，此时性能吞吐量就受到了功能单元运算的限制，CPE值为1。

参考机所能达到的CPE界限如下：

5.4.3 理解combine4的CPE

注意到combine4的CPE与Intel Core i7 Haswell算数运算性能中的延迟基本一致：整型加法为1、乘法为3、浮点加法为3、乘法为5。这可以利用以下数据流图理解：

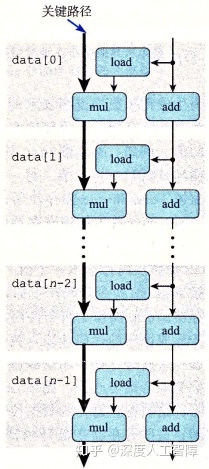
上图解释了乘法的情况，其实把mul改成OP可能更好一点。combine4的for循环存在两个数据相关，一个是i的加法、另一个是acc的乘法。由于存在数据相关，功能单元无法进行流水线。i的加法延迟为1，acc乘法延迟为3（若acc为整型）或者5（浮点型）。 可见acc的运算时长多于i的运算，形成了所谓的关键路径（critical path）。

还需指出，数据流中的关键路径只是提供程序需要周期数的下界，还有很多其他因素会限制性能。比如当我们将左侧的操作变为整数加法时，根据数据流预测的CPE应该为1，但是由于这里的操作变得很快，使得其他操作供应数据的速度不够快，造成实际得到的CPE为1.27。

5.5 那个例子继续引发的血案

之前通过努力，将CPE成功的降低到接近latency bound的水平。但是处理器的能力可以达到throughput bound的水平。于是血案还在继续。。。

k × 1 循环展开的combine5

void combine5(vec_ptr v, data_t *dest)
{
    long i;
    long length = vec_length(v);
    long limit = length-k+1;
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;
    for (i = 0; i < limit; i += k) {
        acc = ((acc OP data[i]) OP data[i+1]) ... OP data[i+k-1];
    }
    for (; i < length; i++) {
        acc = acc OP data[i];
    }
    return acc;
}

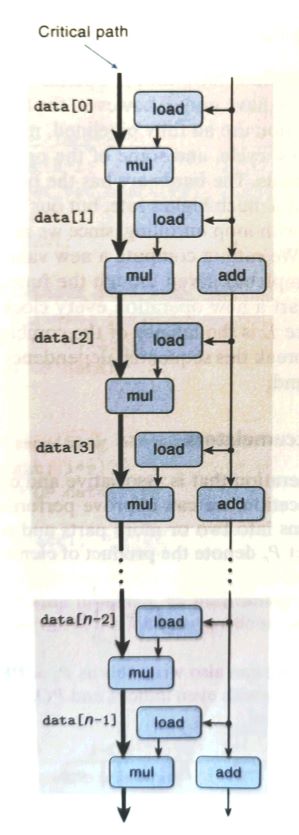
简单的说，combine5通过在每次循环干两倍的活，把n次循环变成了n/2次。然而同样由于数据相关，并没有突破latency bound（acc = ((acc OP data[i]) OP data[i+1]) ... OP data[i+k-1]不断利用acc导致了数据相关）。 只不过是把整数加法成功优化成了延迟界限，这是因为延迟展开能减少不必要的操作的数量（例如循环索引计算和条件分支）。k等于2时的combine5的数据流图如下：

k × k 循环展开的combine6

void combine6(vec_ptr v, data_t *dest)
{
    long i;
    long length = vec_length(v);
    long limit = length-k+1;
    data_t *data = get_vec_start(v);
    data_t acc0 = IDENT;
    data_t acc1 = IDENT;
    ...
    data_t acck_1 = IDENT; //k个变量
  
    for (i=0; i < limit; i+=k) {
        acc0 = acc0 OP data[0];
        acc1 = acc1 OP data[1];
        ...
        acck_1 = acck_1 OP data[k-1]; //更新k个变量
    }  
    for(; i < length; i++) {
        acc0 = acc0 OP data[i];
    }
    *dest = acc0 OP acc1 OP ... OP acck_1;
  }

可见k × k循环展开成功地突破了延迟界限。k等于2的数据流图如下所示：

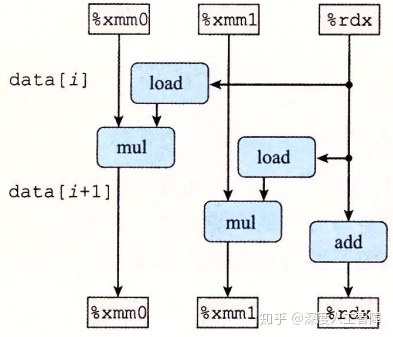
其中，%xmm0保存acc0，%xmm保存%acc1，%rdx保存i。可以发现，我们通过在循环中引入多个变量， 使得原来在同一个循环寄存器中的浮点数乘法运算分配到不同的循环寄存器中，就消除了循环寄存器的数据相关限制， 就可以使用不同的功能单元，或利用功能单元的流水线进行并行计算，就能突破延迟界限。

为了接近吞吐量界限，我们需要使用系统中的所有功能单元，并且保证功能单元的流水线始终是慢的。 所以对于容量为C、延迟为L的操作而言，需要设置 k ≥ C × L（最快每个时钟周期执行一个操作）。

可以看到20 × 20的循环展开性能反而低于10 × 10的循环展开，这是因为k大于寄存器的数目，则中间结果就会保存到内存的堆栈中，使得计算中间结果要反复读写内存，造成性能损失。

改变结合顺序的combine7

之前提及combine5由于acc = ((acc OP data[i]) OP data[i+1]) ... OP data[i+k-1]不断利用acc而导致了数据相关。这个可以通过改成acc = acc OP (data[i] OP (data[i+1]) (... OP data[i+k-1]))来避免数据相关。 将这种修改后的循环展开称做k * 1a展开。其CPE如下：

可以发现kx1a的性能类似于kxk的性能。编译器并不会自动做这种优化，因为浮点数并不满足结合律，虽然整型满足结合律。

5.6 总结

想要提高程序运行速度，可以采取以下几点：

• 采用高效的算法和数据结构
• 减少不必要的函数调用，可利用局部变量
• 减少不必要的内存引用，可利用局部变量
• 循环展开
• 提高指令级并行，如修改乘法结合律
• 利用条件数据传送来代条件控制转移（第三章讨论过）

5.7 尚未提及的几点

利用gprof工具可以确定程序的各个部分需要的时间。这行为叫做程序剖析（Profiling）。似乎valgrind也可以。

加载数据和存储数据也可能破坏程序性能。

        　☆ *　. 　☆
        　　. ∧＿∧　∩　* ☆
        * ☆ ( ・∀・)/ .
        　. ⊂　　 ノ* ☆
        ☆ * (つ ノ .☆
        　　 (ノ